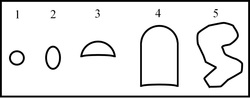
 A variety of bubble shapes which may be found within magmas. Taken from my thesis: Pering, 2015. Over the past 3 years I have delved into a large variety of topics in varying arrays of detail. However, a major theme throughout my work has been the investigation into the fluid dynamics of bubbles, and in particular a feature known as a Taylor bubble (or gas slug) e.g.Wallis (1969) and Bendiksen, (1985). Increasing mass and/or volume of a bubble its shape will naturally change, from a spherical bubble (Wegener and Parlange, 1973) to one that may elongate or deform, through to a cap bubble and then the Taylor bubble. The Figure on the right hand side illustrates this nicely. One of the major activities driven by the Taylor bubble is strombolian volcanism, be it that related to single events (as at Stromboli) or more rapid events, as I have previously observed at Etna.
The Taylor bubble has a number of predictable parameters, including: the distances between the wall and the Taylor bubble edge (termed the falling film), the rise speed of the base of the Taylor bubble, and certain lengths associated with the passage of the bubble - the wake and interaction lengths (Campos and Guedes de Carvalho, 1988). In addition there are a number of dimensionless numbers which help characterise the behaviour of a gas bubble within a fluid, e.g. Reynolds, Morton, Eotvos, and Weber numbers. Within volcanology one area of focus is on the determination of the masses of these Taylor bubbles (i.e. using ultra-violet cameras), which can then be used to work out final lengths and possible burst pressures of the bubbles. All of these parameters above require a set of distinct equations to calculate, which, can sometimes be difficult to locate. There are very few (in fact I didn't find any) resources available online for the calculation of many of these parameters and their calculation often involves the loading up of software such as Matlab. It is for these reasons that I have created an online calculator to enable the calculation of a range of useful (to me and hopefully to others!) dimensionless numbers and Taylor bubble related features. This resource is available here, and for the moment I have called it the "Slug Calculator". It is currently split into two sections. The first "Dimensionless Numbers and Taylor Bubble Parameters" essentially allows the calculation of parameters related to the section title, while the second "Taylor Bubble Mass and Length Inputs/Results" uses pressure, temperature, mass and ratio values (of the common volcanic gases) to estimate a variety of potentially important Taylor Bubble parameters. The calculator is a work in progress, so will be improved and altered as I notice errors or learn how to make improvements! References Bendiksen, K. H., 1985. On the motion of long bubbles in vertical tubes. International Journal of Multiphase Flow 11 (6), 797-812, doi:10.1016/0301-9322(85)90025-4 Campos, J. B. L. M., Guedes de Carvalho, J. R. F., 1988. An experimental study of the wake of gas slugs rising in liquids, Journal of Fluid Mechanics 196, 27-37, doi:10.1017/S0022112088002599 Pering, 2015. Bubbles in Basalts: Measuring and Modelling Basaltic Degassing. PhD Thesis, 2015. University of Sheffield. Wallis, G. B., 1969. One-dimensional two-phase flow. New York, NY: McGraw-Hill Wegener, P. P., Parlange, J. Y., 1973. Spherical-Cap Bubbles. Annual Review of Fluid Mechanics 5, 79-100. doi:10.1146/annurev.fl.05.010173.000455 Comments are closed.
|
  Archives
July 2023
|
RSS Feed